Խաչաձեւ բազմապատկումը երկու հավասարազոր կոտորակների փոփոխական ընդգրկող հավասարումների լուծման միջոց է: Փոփոխականը հանդիսանում է թվերի անհայտ քանակի տեղապահ և խաչաձև բազմապատկումը այն վերածում է պարզ հավասարման ՝ թույլ տալով գտնել տվյալ փոփոխականի արժեքը: Խաչաձեւ բազմապատկումը շատ օգտակար է, երբ ուզում ես համեմատություն կատարել: Ահա թե ինչպես դա անել.
Քայլ
Մեթոդ 1 2 -ից. Մեկ փոփոխականի խաչաձև արտադրանք
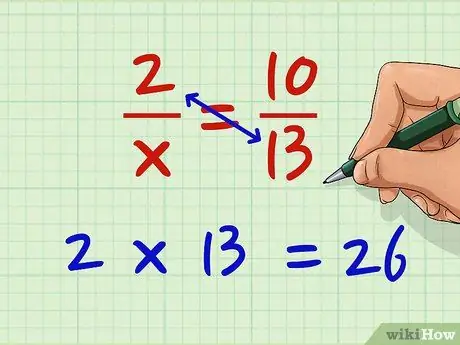
Քայլ 1. Ձախ ձեռքի կոտորակի համարիչը բազմապատկիր աջ մասի հայտարարի հետ:
Ասեք, որ ցանկանում եք լուծել 2/x = 10/13 հավասարումը: Այժմ բազմապատկեք 2 -ը 13.2 x 13 = 26 -ով:
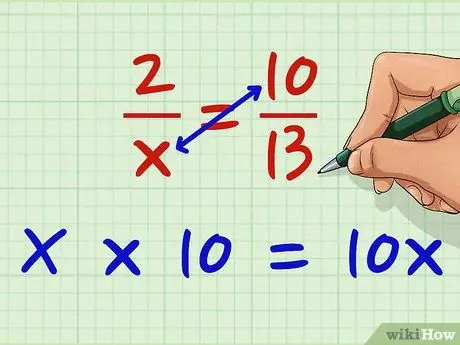
Քայլ 2. Բազմապատկիր աջակտորը ձախակողմյան հայտարարով:
X- ը բազմապատկեք 10 -ով: X * 10 = 10x: Նախ կարող եք հատել այս հատվածը. դա նշանակություն չունի, քանի դեռ երկու համարիչներն էլ անկյունագծով բազմապատկում եք երկու հայտարարների վրա:
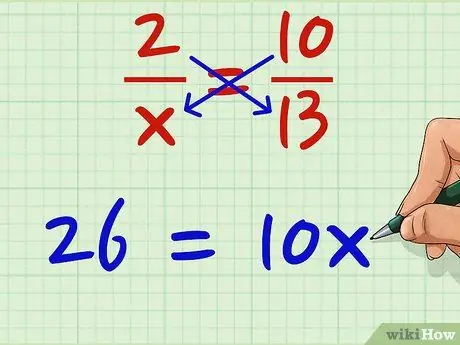
Քայլ 3. Երկու ապրանքները հավասարեցրեք:
26 -ը համարժեք է 10x- ի: 26 = 10x Կարևոր չէ, թե որն է աջից կամ ձախից. լինելով հավասար, կարող եք փոխել նրանց գտնվելու վայրը, քանի դեռ դրանք բոլորը միանգամից տեղափոխել եք:
Այսպիսով, եթե փորձեք գտնել x արժեքը 2/x = 10/13, 2 * 13 = x * 10 կամ 26 = 10x:
Քայլ 4. Գտեք փոփոխականի արժեքը:
Այժմ, երբ ունեք 26 = 10x, կարող եք փորձել գտնել ընդհանուր համարիչ և բաժանել 26 -ը և 10 -ը նույն թվով, որը բաժանում է երկուսն էլ: Քանի որ երկուսն էլ զույգ թվեր են, կարելի է բաժանել 2 -ի; 26/2 = 13 և 10/2 = 5. Մնացածը ՝ 13 = 5x: Այժմ, միայն x- ն վերցնելով, հավասարման երկու կողմերը բաժանեք 5 -ի: Այսպիսով, 13/5 = 5/5 կամ 13/5 = x: Եթե ցանկանում եք պատասխանը տասնորդական տեսքով, կարող եք սկսել ՝ հավասարման երկու կողմերը բաժանելով 10 -ի ՝ ստանալով 26/10 = 10/10 կամ 2,6 = x:
Մեթոդ 2 -ից 2 -ը. Բազմափոփոխ խաչի բազմապատկում
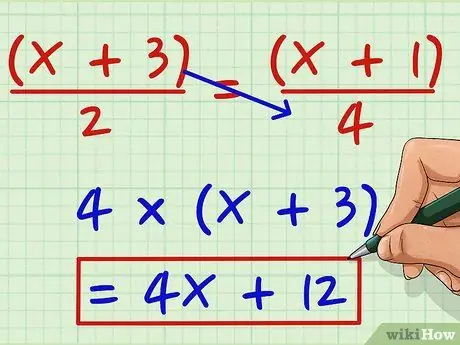
Քայլ 1. Բազմապատկեք ձախ կողմում գտնվող համարիչը ՝ աջ կողմի հայտարարով:
Ասեք, որ ցանկանում եք լուծել հետևյալ հավասարումը. (X + 3)/2 = (x + 1)/4: Բազմապատկել (x + 3) 4 -ով `ստանալով 4 (x + 3): 4 -ով բազմապատկելով ՝ կստանանք 4x + 12:
Քայլ 2. Բազմապատկեք աջ կողմում գտնվող համարիչը ձախ կողմում գտնվող հայտարարով:
Կրկնեք գործընթացը մյուս կողմից: (x+1) x 2 = 2 (x+1): Բազմապատկելով 2 -ով ՝ ստացեք 2x + 2:
Քայլ 3. Երկուսի արտադրյալը հավասար դարձրու և միացրու նույն փոփոխականները:
Այժմ արդյունքը 4x + 12 = 2x + 2 է: Միացրեք x փոփոխականը և հաստատունի հավասարման մյուս կողմում գտնվող հաստատուն:
- Այսպիսով, միավորեք 4x և 2x ՝ երկու կողմերից հանելով 2x: 2x- ից 2x- ը հանելով ՝ մնացորդը 0 կմնա ձախ կողմում, 4x - 2x = 2x, այնպես որ մնացորդը 2x է:
- Այժմ, միավորեք 12 -ը և 2 -ը ՝ երկու կողմերից հանելով 12 -ը: Ձախ կողմում 12 -ից հանեք 12 -ը և արդյունքը 0 է, այնուհետև աջից ՝ 2 -ից հանեք 12 -ը, որպեսզի արդյունքը լինի 2 -12 = -10:
- Մնացածը 2x = -10:
Քայլ 4. Ավարտեք:
Մնում է հավասարման երկու կողմերը բաժանել 2 -ի: 2x/2 = -10/2 = x = -5: Խաչը բազմապատկելուց հետո գտնում ես, որ x = -5: Կարող եք վերադառնալ և ստուգել ձեր աշխատանքը ՝ մուտքագրելով x արժեքը, որը -5 է ՝ համոզվելու համար, որ երկու կողմերն էլ հավասար են: Պարզվեց, որ համարժեք է: Եթե -5 -ը միացնեք սկզբնական հավասարումին, արդյունքը կլինի -1 = -1:
Խորհուրդներ
- Նկատի ունեցեք, որ եթե տարբեր թվեր (ասենք 5) միացնում եք նույն հավասարմանը, արդյունքը կլինի 2/5 = 10/13: Նույնիսկ եթե ձախ կողմը բազմապատկեք ևս 5/5 -ով, կստանաք 10/25 = 10/13, ինչը ակնհայտորեն սխալ է: Այս դեպքը ցույց է տալիս, որ դուք թույլ եք տվել խաչի բազմապատկման սխալ:
- Դուք կարող եք ստուգել ձեր պատասխանը ՝ միացնելով ձեր արդյունքը սկզբնական հավասարման մեջ: Եթե հավասարումը ճշմարիտ հայտարարություն է, օրինակ 1 = 1, ձեր պատասխանը ճիշտ է: Եթե հավասարումը դառնում է կեղծ հայտարարություն, օրինակ `0 = 1, դուք սխալ եք թույլ տվել: Օրինակ, 2, 6 միացրեք հավասարման մեջ այնպես, որ 2/(2, 6) = 10/13: Ձախ կողմը բազմապատկեք 5/5 -ով ՝ ստանալու 10/13 = 10/13: Արդյունքը ճիշտ պնդում է, որը պարզեցվելիս դառնում է 1 = 1, այնպես որ 2, 6 -ը ճիշտ պատասխանն է:
