Չգիտե՞ք ինչպես գծիչ հավասարումներ գծել առանց հաշվիչ օգտագործելու: Բարեբախտաբար, գծային հավասարումների գծագրումը բավականին հեշտ է, եթե գիտեք ինչպես: Մնում է միայն հասկանալ մի քանի բան ձեր հավասարման մասին և կկարողանաք դա անել: Եկ սկսենք.
Քայլ
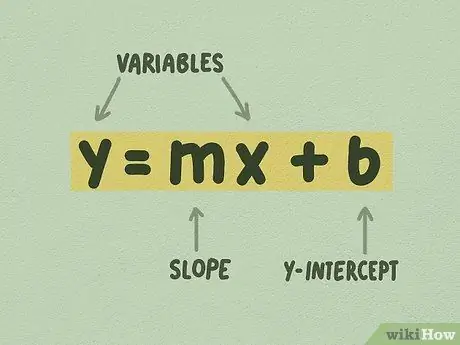
Քայլ 1. Համոզվեք, որ գծային հավասարումը ունի y = mx + b ձև:
Այս ձևը կոչվում է y- ընդհատման ձև և, հավանաբար, ամենահեշտ ձևն է, որն օգտագործվում է գծային հավասարումների գծագրման համար: Պարտադիր չէ, որ հավասարման արժեքը լինի ամբողջ թիվ: Հաճախ դուք կտեսնեք այսպիսի հավասարում ՝ y = 1/4x + 5, որտեղ 1/4 -ը m է, իսկ 5 -ը ՝ b:
- մ կոչվում է «թեքություն», կամ երբեմն «գրադիենտ»: Թեքությունը սահմանվում է որպես կողմի աճ, կամ y- ի փոփոխություն բաժանված x- ի փոփոխությամբ:
- b- ը սահմանվում է որպես «y-intercept»: Y- ընդհատումը այն կետն է, որտեղ գիծը հատում է Y- առանցքը:
- x և y փոփոխական են: Դուք կարող եք լուծել որոշակի x արժեքի համար, օրինակ, եթե ունեք y կետ և գիտեք m և b արժեքները: Այնուամենայնիվ, x- ը երբեք չունի միայն մեկ արժեք. Դրա արժեքը փոխվում է, երբ տողը բարձրանում կամ նվազում է:
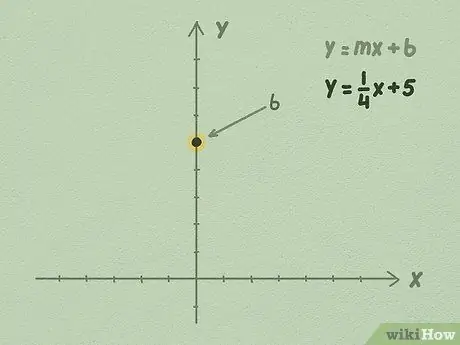
Քայլ 2. Y առանցքի վրա նկարիր b թիվը:
Ձեր b արժեքը միշտ կլինի ռացիոնալ թիվ: Ինչ էլ որ լինի b թիվը, գտեք դրա արժեքը Y առանցքի վրա և թիվը տեղադրեք ուղղահայաց առանցքի մի կետում:
Օրինակ, եկեք օգտագործենք y = 1/4x + 5 հավասարումը: Քանի որ վերջին թիվը b է, մենք գիտենք, որ b- ն հավասար է 5 -ի: Y առանցքի վրա շարժվեք 5 կետով և նշեք կետերը: Սա այն է, որտեղ ձեր ուղիղ գիծը հատելու է Y առանցքը:
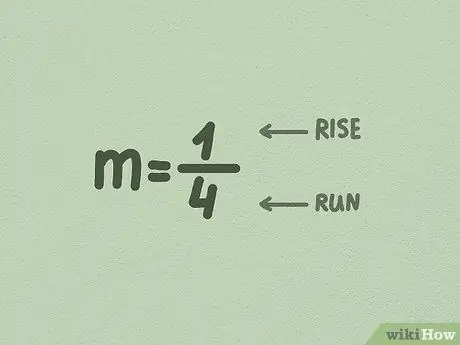
Քայլ 3. m- ը վերածիր կոտորակի:
Հաճախ x- ի դիմաց թիվն արդեն կոտորակ է, ուստի այն փոխելու կարիք չկա: Բայց եթե ոչ, պարզապես փոխեք այն ՝ տեղադրելով m արժեքը 1 թվի տակ:
- Առաջին թիվը (համարիչը) աճի աճի աճն է ՝ բաժանված կողմի վրա: Այս թիվը ցույց է տալիս, թե որքան հեռու է գիծը բարձրանում կամ ուղղահայաց:
- Երկրորդ թիվը (հայտարարը) աճման մեջ գտնվող կողմն է ՝ բաժանված կողմի վրա: Այս թիվը ցույց է տալիս, թե որքան հեռու է տողը շարժվում կողքով կամ հորիզոնական:
- Օրինակ:
- 4/1 թեքությունը յուրաքանչյուր 1 կետի դիմաց 4 միավոր բարձրանում է դեպի կողմ:
- -2/1 թեքությունը յուրաքանչյուր 1 կետի դիմաց 2 կետ իջնում է դեպի կողմ:
- 1/5 թեքությունը յուրաքանչյուր 5 կետի դիմաց 1 կետ բարձրացնում է դեպի կողմ:
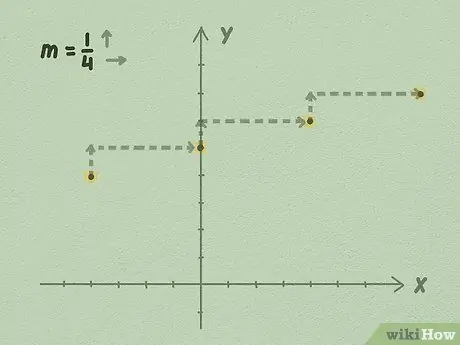
Քայլ 4. Սկսեք երկարացնել b- ից գիծը ՝ օգտագործելով թեքությունը, կամ վերև ՝ կիսելով կողքով:
Սկսեք ձեր b արժեքից. Մենք գիտենք, որ հավասարումը անցնում է այս կետից: Երկարացրեք գիծը `վերցնելով ձեր թեքությունը և օգտագործելով դրա արժեքը` հավասարման կետերը ստանալու համար:
- Օրինակ ՝ օգտագործելով վերևի նկարազարդումը, կարող եք տեսնել, որ յուրաքանչյուր 1 կետի դիմաց գիծը 4 կետով շարժվում է աջ: Դա տեղի է ունենում, քանի որ գծի թեքությունը 1/4 է: Դուք գիծը երկարացնում եք անորոշ ժամանակով երկու կողմերի վրա ՝ շարունակելով սպառումը ՝ բաժանված կողմի վրա ՝ գծի գծապատկերում:
- Թեքությունը դրական է վեր շարժվելիս, մինչդեռ թեքությունը բացասական է ներքև շարժվելիս: Օրինակ ՝ -1/4 թեքությունը, յուրաքանչյուր 4 կետի համար 1 կետով կիջնի կողքի:
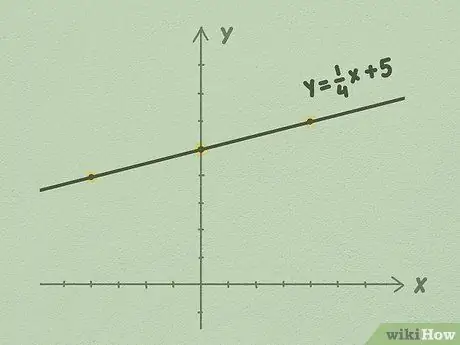
Քայլ 5. Շարունակեք երկարացնել գիծը ՝ օգտագործելով գծիչ և համոզվեք, որ որպես ուղեցույց օգտագործեք թեքությունը, մ:
Երկարացրեք տողը անորոշ ժամանակով, և դուք կավարտեք գծային հավասարման գծագրումը: Բավականին հեշտ է, այնպես չէ՞:
