- Հեղինակ Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:35.
- Վերջին փոփոխված 2025-01-23 12:20.
Օպտիկական գործիքների ուսումնասիրության ժամանակ ոսպնյակի նման օբյեկտի «խոշորացումը» ձեր տեսած պատկերի բարձրության հարաբերությունն է օբյեկտի իրական բարձրությանը: Օրինակ, ոսպնյակը, որը կարող է առարկան դարձնել շատ մեծ, ունի «բարձր» խոշորացման գործոն, մինչդեռ ոսպնյակը, որը օբյեկտին փոքր է դարձնում, ունի «ցածր» խոշորացման գործոն: Օբյեկտի մեծացման բանաձևը սովորաբար հաշվարկվում է բանաձևի միջոցով M = (ժես/ժo) = -(մես/դo), որտեղ M = խոշորացում, ժես = պատկերի բարձրությունը, ժo = օբյեկտի բարձրությունը, և դես եւ Դo = պատկերի և օբյեկտի հեռավորությունը:
Քայլ
Մեթոդ 1 2 -ից. Մեկ ոսպնյակի խոշորացման հաշվարկում
Նշումներ. Ա համընկնող ոսպնյակ ավելի լայն `կենտրոնում, քան եզրերին (խոշորացույցի նման): ա տարբերվող ոսպնյակ ծայրերում ավելի լայն, քան կենտրոնում (ամանի նման): Երկու ոսպնյակների խոշորացման հաշվարկը նույնն է, հետ մեկ կարևոր բացառություն. Կտտացրեք այստեղ ՝ ուղղակիորեն տարբերվող ոսպնյակների բացառություններին:
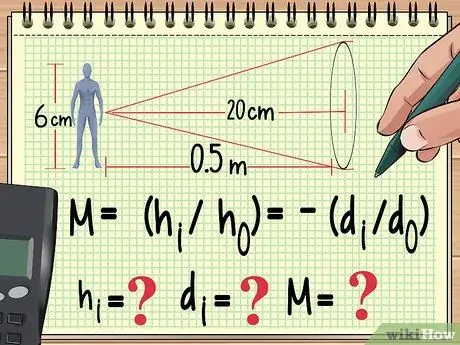
Քայլ 1. Սկսեք ձեր հավասարումից և արդեն իմացած փոփոխականներից:
Ինչպես ֆիզիկայի ցանկացած այլ խնդիր, այնպես էլ խոշորացման խնդրի լուծման ուղին է գրել այն հավասարումը, որը կօգտագործես այն հաշվարկելու համար: Այստեղից կարող եք հետընթաց աշխատել ՝ գտնելու համար օգտագործվող հավասարումից չգտած փոփոխականի արժեքը:
-
Օրինակ, ենթադրենք, 6 սմ բարձրությամբ տիկնիկը տեղադրված է a- ից մեկ մետր հեռավորության վրա համընկնող ոսպնյակ 20 սմ կիզակետային երկարությամբ: Եթե ցանկանում ենք հաշվարկել խոշորացումը, պատկերի բարձրությունը և պատկերի հեռավորությունը, կարող ենք սկսել գրել մեր հավասարումը հետևյալ կերպ.
-
- M = (ժես/ժo) = -(մես/դo)
-
- Այժմ մենք գիտենք հo (տիկնիկի բարձրությունը) և դo (տիկնիկի հեռավորությունը ոսպնյակից): Մենք նաև գիտենք ոսպնյակի կիզակետային երկարությունը, որը այս հավասարման մեջ չէ: Մենք կհաշվենք ժես, դես, և Մ.

Քայլ 2. Օգտագործելով ոսպնյակի հավասարումը ՝ d ստանալու համարես.
Եթե գիտեք ձեր խոշորացվող օբյեկտից հեռավորությունը և ոսպնյակի կիզակետային երկարությունը, ձևավորված պատկերից հեռավորությունը հաշվարկելը ոսպնյակի հավասարման միջոցով շատ հեշտ է: Ոսպնյակի հավասարումն է 1/f = 1/օրo + 1/օրես, որտեղ f = ոսպնյակի կիզակետային երկարությունը:
-
Այս օրինակի խնդրում մենք կարող ենք օգտագործել ոսպնյակի հավասարումը ՝ d- ն հաշվարկելու համարես. Մուտքագրեք f և d արժեքներըես ապա լուծիր հավասարումը.
-
- 1/f = 1/օրo + 1/օրես
- 1/20 = 1/50 + 1/օրես
- 5/100 - 2/100 = 1/օրես
- 3/100 = 1/օրես
- 100/3 = դես = 33,3 սմ
-
- Ոսպնյակի կիզակետային երկարությունը ոսպնյակի կենտրոնից մինչև այն կետն է, որտեղ լույսը փոխանցվում է կիզակետում: Եթե երբեւէ խոշորացույցով լույսը կենտրոնացրել եք այրվող մրջյունների վրա, ապա դա տեսել եք: Դասի հարցերում սովորաբար տրվում է այս թեժ կետի մեծությունը: Իրական կյանքում այդ բնութագրերը սովորաբար գրվում են ոսպնյակի վրա տեղադրված պիտակի վրա:

Քայլ 3. Հաշվարկը ժես.
Հաշվելուց հետո դo եւ Դես, կարող եք հաշվարկել խոշորացված օբյեկտի բարձրությունը և ոսպնյակի խոշորացումը: Ոսպնյակի խոշորացման հավասարման մեջ նկատեք երկու հավասար նշաններ (M = (ժես/ժo) = -(մես/դo)) - սա նշանակում է, որ այս հավասարման բոլոր մասերը հավասար են միմյանց, այնպես որ կարող ենք հաշվարկել M և hես ինչ կարգով ուզում ենք:
-
Այս օրինակի խնդրի համար մենք կարող ենք հաշվարկել ժես սրա նման:
-
- (ժես/ժo) = -(մես/դo)
- (ժես/6) = -(33, 3/50)
- ժես = -(33, 3/50) x 6
- ժես = - 3, 996 սմ
-
- Նկատի ունեցեք, որ այստեղ օբյեկտի բարձրությունը բացասական է, ինչը ցույց է տալիս, որ պատկերը, որը մենք հետագայում կտեսնենք, շրջված կլինի (վերևից ներքև):

Քայլ 4. Հաշվարկելով Մ
Դուք կարող եք հաշվարկել վերջին փոփոխականը հավասարման միջոցով (դես/դo) կամ (ժես/ժo).
-
Հետևյալ օրինակում, թե ինչպես հաշվարկել M- ն, հետևյալն է.
-
- M = (ժես/ժo)
-
M = (-3, 996/6) = - 0, 666
-
-
Արդյունքը նույնպես նույնը կլինի, երբ հաշվարկվում է d արժեքը.
-
- M = -(մես/դo)
- M = -(33, 3/50) = - 0, 666
-
- Նշենք, որ խոշորացումը չունի միավորի պիտակ:
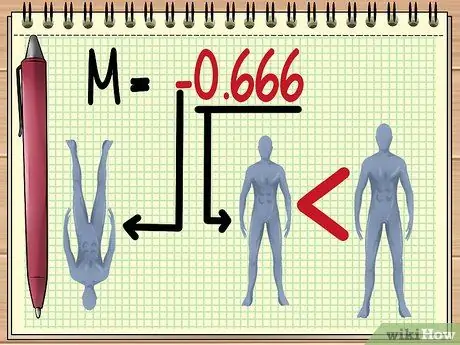
Քայլ 5. Հասկանալով M արժեքը:
M արժեքի մեծությունը ստանալուց հետո կարող եք գնահատել մի քանի բան այն պատկերի մասին, որը կտեսնեք ոսպնյակի միջով, այն է `
-
Չափը:
Որքան մեծ լինի M- ի «բացարձակ արժեքը», այնքան մեծ կլինի ոսպնյակի հետ դիտվող օբյեկտը: M արժեքը 0 -ից 1 -ը ցույց է տալիս, որ օբյեկտը ավելի փոքր տեսք կունենա:
-
Օբյեկտի կողմնորոշում:
Բացասական արժեքը ցույց է տալիս, որ ձևավորված պատկերը հակադարձ կլինի:
- Այստեղ բերված օրինակում, -0.666 արժեքը M նշանակում է, որ ըստ առկա փոփոխականի արժեքի, տիկնիկի ստվերը տեսանելի կլինի: գլխիվայր և երկու երրորդով փոքր իրական չափից.
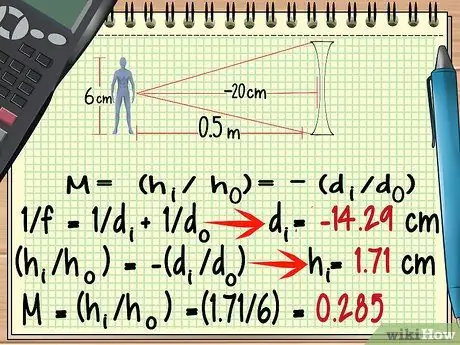
Քայլ 6. Տարբերվող ոսպնյակների համար օգտագործեք բացասական կիզակետ:
Չնայած տարբերվող ոսպնյակի ձևը շատ տարբեր է կոնվերգենցիոն ոսպնյակի ձևից, դուք կարող եք հաշվարկել դրա խոշորացումը ՝ օգտագործելով վերը նշված բանաձևը: Բացառությունները, որոնք պետք է հիշել, կան Տարբերվող ոսպնյակի կիզակետը բացասական է:
Վերոնշյալ խնդրի օրինակում դա կազդի այն պատասխանի վրա, որը դուք կստանաք հաշվարկելիս դես, այնպես որ համոզվեք, որ ուշադրություն դարձնեք սրան:
-
Եկեք վերամշակենք վերը նշված խնդրի խնդիրը, միայն հիմա մենք օգտագործում ենք կիզակետային հեռավորությամբ տարատեսակ ոսպնյակ - 20 սմ
Մնացած փոփոխականները մնում են նույն արժեքը:
-
Առաջին հերթին, մենք կհաշվենք դես օգտագործելով ոսպնյակի հավասարումը.
-
- 1/f = 1/օրo + 1/օրես
- 1/-20 = 1/50 + 1/օրես
- -5/100 - 2/100 = 1/օրես
- -7/100 = 1/օրես
- -100/7 = դես = - 14, 29 սմ
-
-
Այժմ մենք կհաշվարկենք ժես և M ՝ d արժեքովես նորը
-
- (ժես/ժo) = -(մես/դo)
- (ժես/6) = -(-14, 29/50)
- ժես = -(- -14, 29/50) x 6
- ժես = 1, 71 սմ
- M = (ժես/ժo)
- M = (1, 71/6) = 0, 285
-
Մեթոդ 2 2 -ից. Բազմակի ոսպնյակների խոշորացման հաշվարկ
Երկու ոսպնյակների պարզ մեթոդ
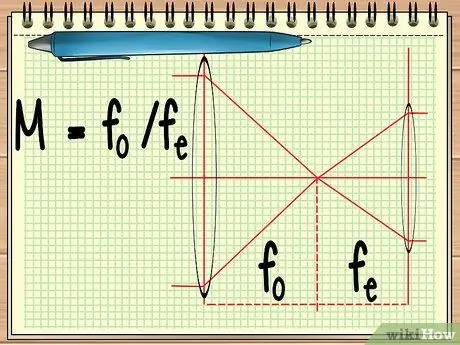
Քայլ 1. Հաշվիր երկու ոսպնյակների կիզակետը:
Երբ օգտագործում եք գործիք, որը բաղկացած է կողք կողքի դասավորված երկու ոսպնյակներից (օրինակ ՝ աստղադիտակ կամ զույգ հեռադիտակ), այն ամենը, ինչ պետք է պարզել, երկու ոսպնյակների առանցքային կետն է ՝ երկու ոսպնյակների ընդհանուր մեծացումը հաշվարկելու համար: սա կարելի է հաշվարկել M = f պարզ հավասարմամբo/զե.
Հավասարում, զo օբյեկտիվ ոսպնյակի կիզակետն է և զե ակնաբույժի կիզակետն է: Օբյեկտիվ ոսպնյակն այն մեծ ոսպնյակն է, որը մոտ է օբյեկտին, մինչդեռ աչքի ոսպնյակն այն ոսպնյակն է, որը գտնվում է դիտորդի աչքին մոտ:

Քայլ 2. Տեղադրեք եղած տեղեկատվությունը M = f հավասարման մեջo/զե.
Երկու ոսպնյակների կիզակետն ունենալուց հետո դրանք շատ հեշտ է հաշվարկել, Ստացված պատասխանը գործիքի ընդհանուր խոշորացումն է:
-
Օրինակ, ենթադրենք մի պարզ աստղադիտակ, գրված է, որ օբյեկտիվ ոսպնյակի կիզակետը 10 սմ է, իսկ ակնաբույսի կիզակետը ՝ 5 սմ, այնուհետև խոշորացումը ՝ 10/5 = 2.
Բարդ մեթոդ
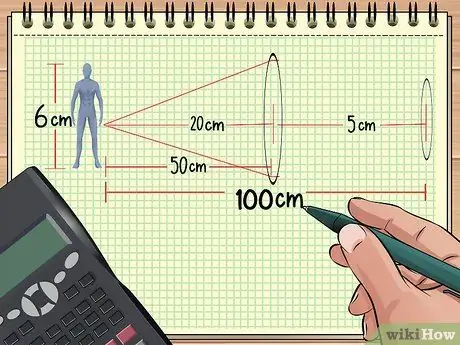
Քայլ 1. Հաշվիր ոսպնյակների և օբյեկտի միջև հեռավորությունը:
Եթե ունեք օբյեկտիվի առջև անընդմեջ դասավորված երկու ոսպնյակ, ընդհանուր խոշորացումը կարող է հաշվարկվել, եթե իմանաք ոսպնյակներից մինչև օբյեկտ հեռավորությունը, օբյեկտի չափը և երկու ոսպնյակների կիզակետը: Մնացածը նույնպես կարող է հաշվարկվել:
Օրինակ ՝ ենթադրենք, որ մենք դասավորում ենք օբյեկտներն ու ոսպնյակները, ինչպես վերը նշված 1 -ին խնդրի դեպքում: Այժմ, երկրորդ ոսպնյակը կիզակետով 5 սմ տեղադրեք առաջին ոսպնյակից 50 սմ հեռավորության վրա (տիկնիկից 100 սմ): Դրանից հետո մենք կհաշվարկենք ընդհանուր խոշորացումը `ձեռք բերված տեղեկատվության միջոցով:
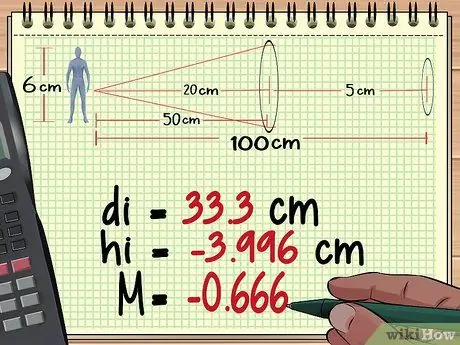
Քայլ 2. Հաշվիր օբյեկտի հեռավորությունը, բարձրությունը և խոշորացումը 1 ոսպնյակից:
Բազմակի ոսպնյակների խոշորացման հաշվարկման առաջին մասը նույնն է, ինչ մեկ ոսպնյակի խոշորացումը հաշվարկելը: Սկսեք օբյեկտին ամենամոտ ոսպնյակից, օգտագործեք ոսպնյակի հավասարումը `ձևավորված պատկերից հեռավորությունը գտնելու համար, այնուհետև օգտագործեք խոշորացման հավասարումը` պատկերի բարձրությունն ու խոշորացումը գտնելու համար: Կտտացրեք այստեղ ՝ ոսպնյակների խոշորացման ավելի շատ հաշվարկներ դիտելու համար:
-
Վերոնշյալ մեթոդ 1 -ի մեր հաշվարկներից մենք գտնում ենք, որ առաջին ոսպնյակը տալիս է նույնքան բարձր պատկեր - 3, 996 սմ, հեռավորություն 33.3 սմ ոսպնյակի հետևում և մեծացման դեպքում - 0, 666.
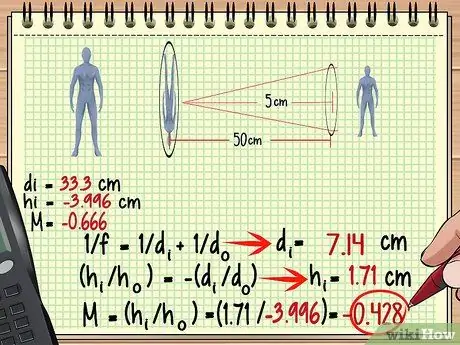
Քայլ 3. Օգտագործեք առաջին ոսպնյակի պատկերը որպես երկրորդ ոսպնյակի օբյեկտ:
Այժմ երկրորդ ոսպնյակի խոշորացում, բարձրություն և ավելին գտնելը շատ հեշտ է. Պարզապես օգտագործեք նույն մեթոդը, որն օգտագործել եք առաջին ոսպնյակի դեպքում, միայն թե այս անգամ պատկերը վերաբերեք որպես օբյեկտի: Հիշեք, որ երկրորդ ոսպնյակի պատկերի հեռավորությունը միշտ չէ, որ նույն օբյեկտի հեռավորությունն է առաջին ոսպնյակից:
-
Վերոնշյալ օրինակում, քանի որ պատկերը ձևավորվել է առաջին ոսպնյակի հետևում 33,3 սմ հեռավորության վրա, հեռավորությունը 50-33,3 = է 16,7 սմ երկրորդ ոսպնյակի դիմաց: Եկեք օգտագործենք այս չափումը և երկրորդ ոսպնյակի կիզակետային երկարությունը `գտնելու երկրորդ ոսպնյակի կողմից ձևավորված պատկերը:
-
- 1/f = 1/օրo + 1/օրես
- 1/5 = 1/16, 7 + 1/օրես
- 0, 2 - 0, 0599 = 1/օրես
- 0, 14 = 1/օրես
- դես = 7, 14 սմ
-
-
Այժմ մենք կարող ենք հաշվարկել ժես իսկ M երկրորդ ոսպնյակի համար.
-
- (ժես/ժo) = -(մես/դo)
- (ժես/-3, 996) = -(7, 14/16, 7)
- ժես = -(0, 427) x -3, 996
- ժես = 1, 71 սմ
- M = (ժես/ժo)
- M = (1, 71/-3, 996) = - 0, 428
-
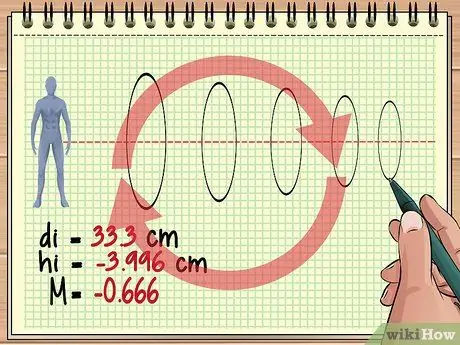
Քայլ 4. Շարունակեք այսպես հաշվարկել լրացուցիչ ոսպնյակների համար:
Այս հիմնական մոտեցումը նույնն է, եթե օբյեկտի դիմաց շարված են երեք, չորս կամ հարյուրավոր ոսպնյակներ: Յուրաքանչյուր ոսպնյակի համար դիտեք նախորդ ոսպնյակի պատկերը որպես օբյեկտ և օգտագործեք ոսպնյակի հավասարումը և խոշորացման հավասարումը `ձեր ուզած պատասխանը գտնելու համար:
Հիշեք, որ յուրաքանչյուր հաջորդ ոսպնյակ կարող է շարունակաբար շրջել ձևավորված պատկերը: Օրինակ, ավելի վաղ ստացված խոշորացման արժեքը (-0, 428) ցույց է տալիս, որ պատկերը, որը մենք պատրաստվում ենք տեսնել, օբյեկտի իրական չափի մոտավորապես 4/10 է, բայց ուղղահայաց, քանի որ նախորդ ոսպնյակի պատկերը շրջված է:
Խորհուրդներ
- Հեռադիտակները սովորաբար տալիս են խոշորացման բնութագրերի բացատրությունը մի քանի անգամ մեկ այլ թվի տեսքով: Օրինակ, հեռադիտակները կարող են նշվել որպես 8x25 կամ 8x40: Այդպես գրելիս առաջին թիվը երկդիտակների խոշորացումն է: Կարևոր չէ, նույնիսկ եթե բերված օրինակում երկու թվերը տարբեր են մեծությամբ, երկու հեռադիտակներն ունեն 8 անգամ խոշորացում: Երկրորդ թիվը ցույց է տալիս, թե որքան պարզ պատկեր կստեղծվի հեռադիտակով:
- Հիշեք, որ միայնակ ոսպնյակների համար լուպի դեպքում խոշորացումը բացասական կլինի, եթե օբյեկտի հեռավորությունը ավելի մեծ լինի, քան ոսպնյակի կիզակետային երկարությունը: Սա չի նշանակում, որ ձևավորված պատկերը ավելի փոքր կլինի: Այս դեպքում մեծացումը դեռ տեղի է ունենում, բայց ձևավորված պատկերը դիտորդը կտեսնի գլխիվայր (վերևից ներքև):






